Redesign Kanji Character by using Bezier and Wang-Ball Curves
DOI:
https://doi.org/10.37934/picl.1.1.1124Keywords:
Curves, surfaces, kanji calligraphy, Bezier, degree elevationAbstract
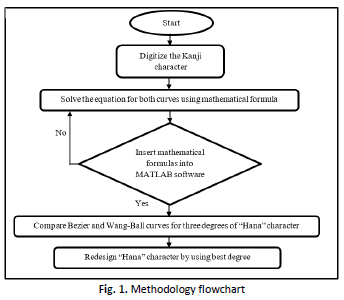
Mathematical expressions can be used in computer-aided geometric design to construct surfaces and curves. This study depicted a 2D object's outline, such as a Kanji character. Kanji calligraphy suggests the Kanji character that represents actual objects. The art of calligraphy is distinct and can only be created by a skilled individual. Kanji calligraphy can be vectorized and saved in digital format to conserve the arts for future use. This study compares the degree elevation of the Bezier and Wang ball curves based on the Kanji calligraphy character "Hana" and uses the curves to rebuild "Hana." The original scanned image of the "Hana" character is compared to the degree elevation for both the Wang ball curve and the Bezier curve methods after Bernstein polynomials are used in the MATLAB software. The degree is assessed up to the fourth degree. The character's redesign will be based on the comparison's best degree. The time it takes to compute the curves is also noted. With a computation time of 0.2094 seconds, the result indicates that the degree four of the Bezier curve is the optimal curve to employ for redesigning the "Hana" character. Since degree four Bezier curves required the least amount of time to construct and demonstrate that Bezier curves are far simpler than Wang ball curves, it can be said that this degree is the greatest choice for redesigning the "Hana" character.
Downloads
References
[1] Said Mad Zain, Syed Ahmad Aidil Adha, Md Yushalify Misro, and Kenjiro T. Miura. "Generalized fractional Bézier curve with shape parameters." Mathematics 9, no. 17 (2021): 2141. https://doi.org/10.3390/math9172141 DOI: https://doi.org/10.3390/math9172141
[2] Alaidroos, Hussain A., Ahmed Kherd, and Salim Bamsaoud. "A Numerical scheme to Solve Boundary Value Problems Involving Singular Perturbation." Baghdad Science Journal 20, no. 6 (Suppl.) (2023): 2521-2521. https://doi.org/10.21123/bsj.2023.6409 DOI: https://doi.org/10.21123/bsj.2023.6409
[3] Ameer, Moavia, Muhammad Abbas, Madiha Shafiq, Tahir Nazir, and Asnake Birhanu. "Generalized Bézier-like model and its applications to curve and surface modeling." Plos one 19, no. 6 (2024): e0303340. https://doi.org/10.1371/journal.pone.0303340 DOI: https://doi.org/10.1371/journal.pone.0303340
[4] Arslan, Ömür, and Aron Tiemessen. "Adaptive bézier degree reduction and splitting for computationally efficient motion planning." IEEE Transactions on Robotics 38, no. 6 (2022): 3655-3674. https://doi.org/10.1109/TRO.2022.3187296 DOI: https://doi.org/10.1109/TRO.2022.3187296
[5] Bawono, B., T. Yuniarto, C. E. P. Sanusi, S. Felasari, O. K. W. Widyanarka, and P. W. Anggoro. "Optimization of virtual design and machining time of the mold master ceramic jewelry products with Indonesian batik motifs." Frontiers in Mechanical Engineering 9 (2024): 1276063. https://doi.org/10.3389/fmech.2023.1276063 DOI: https://doi.org/10.3389/fmech.2023.1276063
[6] Bhatti, Abdul Hadi, and Sharmila Binti Karim. "Solving Ordinary Differential Equations (ODEs) Using Least Square Method Based on Wang Ball Curves." Mathematics and Statistics 10, no. 1 (2022): 74-87. https://doi.org/10.13189/ms.2022.100106 DOI: https://doi.org/10.13189/ms.2022.100106
[7] Eze, Monday, Charles Okunbor, Deborah Aleburu, Olubukola Adekola, Ibrahim Ramon, Nneka Richard-Nnabu, Oghenetega Avwokuruaye, Abisola Olayiwola, Rume Yoro, and Esomu Solomon. "Graphics Evolutionary Computations in Higher Order Parametric Bezier Curves." Computer Systems Science & Engineering 41, no. 2 (2022). https://doi.org/10.32604/csse.2022.020835 DOI: https://doi.org/10.32604/csse.2022.020835
[8] Farin, Gerald. "Triangular bernstein-bézier patches." Computer Aided Geometric Design 3, no. 2 (1986): 83-127. https://doi.org/10.1016/0167-8396(86)90016-6 DOI: https://doi.org/10.1016/0167-8396(86)90016-6
[9] Hamza, Yusuf Fatihu, Mukhtar Fatihu Hamza, Abedallah Rababah, and Salisu Ibrahim. "Geometric Degree Reduction of Wang–Ball Curves." Applied Computational Intelligence and Soft Computing 2023, no. 1 (2023): 5483111. https://doi.org/10.1155/2023/5483111 DOI: https://doi.org/10.1155/2023/5483111
[10] Hu, Gang, Min Li, and Jingyu Zhong. "Combined cubic generalized ball surfaces: Construction and shape optimization using an enhanced JS algorithm." Advances in Engineering Software 176 (2023): 103404. https://doi.org/10.1016/j.advengsoft.2022.10340 DOI: https://doi.org/10.1016/j.advengsoft.2022.103404
[11] Hu, Gang, and Bo Du. "Ball Said-Ball curve: Construction and its geometric algorithms." Advances in Engineering Software 174 (2022): 103334. https://doi.org/10.1016/j.advengsoft.2022.103334
[12] Karateke, S., R. Akalin, and M. Gümüş. "The evolution of Bézier curves in computer-aided geometric design (CAGD): a systematic review." Research on Mathematics and Science-II. Özgür Publications (2023). https://doi.org/10.58830/ozgur.pub165.c677 DOI: https://doi.org/10.58830/ozgur.pub165.c677
[13] Mahmoud, W. M., M. A. Soliman, and Esraa M. Mohamed. "Investigation on Isotropic Bezier Sweeping Surface" IBSS" with Bishop Frame." (2023). https://doi.org/10.13189/ms.2023.110216
[14] Ramanantoanina, Andriamahenina, and Kai Hormann. "Shape control tools for periodic Bézier curves." Computer aided geometric design 103 (2023): 102193. https://doi.org/10.1016/j.cagd.2023.102193 DOI: https://doi.org/10.1016/j.cagd.2023.102193
[15] Sharma, Reenu. "Applications of Quartic Trigonometric Bézier Curves and Surfaces in CAGD." Journal of Research and Analytical Reviews (IJRAR) 6, no. 2 (2019): 462-475. https://doi.org/10.6084/m9.doi.one.IJRAR19K1234
[16] Rababah, Abedallah, and Moath Jaradat. "Approximating offset curves using bézier curves with high accuracy." International Journal of Electrical and Computer Engineering 10, no. 2 (2020): 1648-1654. http://doi.org/10.11591/ijece.v10i2.pp1648-1654 DOI: https://doi.org/10.11591/ijece.v10i2.pp1648-1654
[17] Shams, Sarah Atef, Olfat Shawki Mohamed, and Tetsuya Sato. "Integrating Arabic and Japanese Calligraphy in Innovative designs for Fashion A Comparative Study of Diwani and Kanji Calligraphy." International Design Journal 9, no. 1 (2019): 273-281. http://doi.org/10.21608/idj.2019.84068 DOI: https://doi.org/10.21608/idj.2019.84068
[18] Hu, Shi-Min, Guo-Zhao Wang, and Tong-Guang Jin. "Properties of two types of generalized Ball curves." Computer-Aided Design 28, no. 2 (1996): 125-133. https://doi.org/10.1016/0010-4485(95)00047-X DOI: https://doi.org/10.1016/0010-4485(95)00047-X
[19] Mahmoud, W. M., M. A. Soliman, and Esraa M. Mohamed. "Investigation on Isotropic Bezier Sweeping Surface" IBSS" with Bishop Frame." (2023). https://doi.org/10.13189/ms.2023.110216 DOI: https://doi.org/10.13189/ms.2023.110216
[20] Wang, GuoJin. "Ball curve of high degree and its geometric properties." Appl. Math.: A Journal of Chinese Universities 2 (1987): 126-140. https://doi.org/10.1016/j.advengsoft.2022.103334 DOI: https://doi.org/10.1016/j.advengsoft.2022.103334
[21] Wei, Jin Pa, Mohammad Izat Emir Zulkifly, and Taufiq Khairi Ahmad Khairuddin. "Biquartic Hesitant Fuzzy Bézier Surface Approximation Model with Its Visualization." Semarak International Journal of Fundamental and Applied Mathematics 3, no. 1 (2024): 1-10. https://doi.org/10.37934/sijfam.3.1.110 DOI: https://doi.org/10.37934/sijfam.3.1.110
[22] Zheng, Jiaoyue, Xiaomin Ji, Zhaozhao Ma, and Gang Hu. "Construction of local-shape-controlled quartic generalized said-ball model." Mathematics 11, no. 10 (2023): 2369. https://doi.org/10.3390/math11102369 DOI: https://doi.org/10.3390/math11102369